pbessolve

The tool pbessolve can solve a PBES. The solution is printed as true or false on the command line output. If the property encoded in the PBES holds, in addition a witness can be constructed, and if the property does not hold a counter example can be constructed. We refer to the witness or counter example as the evidence of a property.

If the PBES was constructed via lps2pbes, then the evidence is an LPS that is a submodel of the LPS that was passed to lps2pbes. If the PBES was constructed via lts2pbes, then the evidence is an LTS that is a submodel of the LTS that was passed to lts2pbes. The evidence is written to a file named <<pbesfile>>.evidence.lps or <<pbesfile>>.evidence.lts. A different name can be specified using the command line option –evidence-file.

A counter example for the “infinitely often enabled then infinitely often taken” property of the ABP protocol can be generated as follows:

mcrl22lps abp.mcrl2 abp.lps
lps2pbes -v -c -f infinitely_often_enabled_then_infinitely_often_taken.mcf abp.lps abp.pbes
pbessolve -v --file=abp.lps abp.pbes
lps2lts abp.pbes.evidence.lps abp.pbes.evidence.lts
ltsgraph abp.pbes.evidence.lts

Note that lps2pbes is called with the option -c to include counter example information in the generated PBES. Also note that the specification abp.lps that was used to create the PBES is passed as an argument to pbessolve with the option –file. It is needed to construct the counter example.

Similarly it can be done starting from an LTS instead of an LPS:

mcrl22lps abp.mcrl2 abp.lps
lps2lts abp.lps abp.lts
lts2pbes -v -c -f infinitely_often_enabled_then_infinitely_often_taken.mcf abp.lts abp.pbes
pbessolve -v --file=abp.lts abp.pbes
ltsgraph abp.pbes.evidence.lts

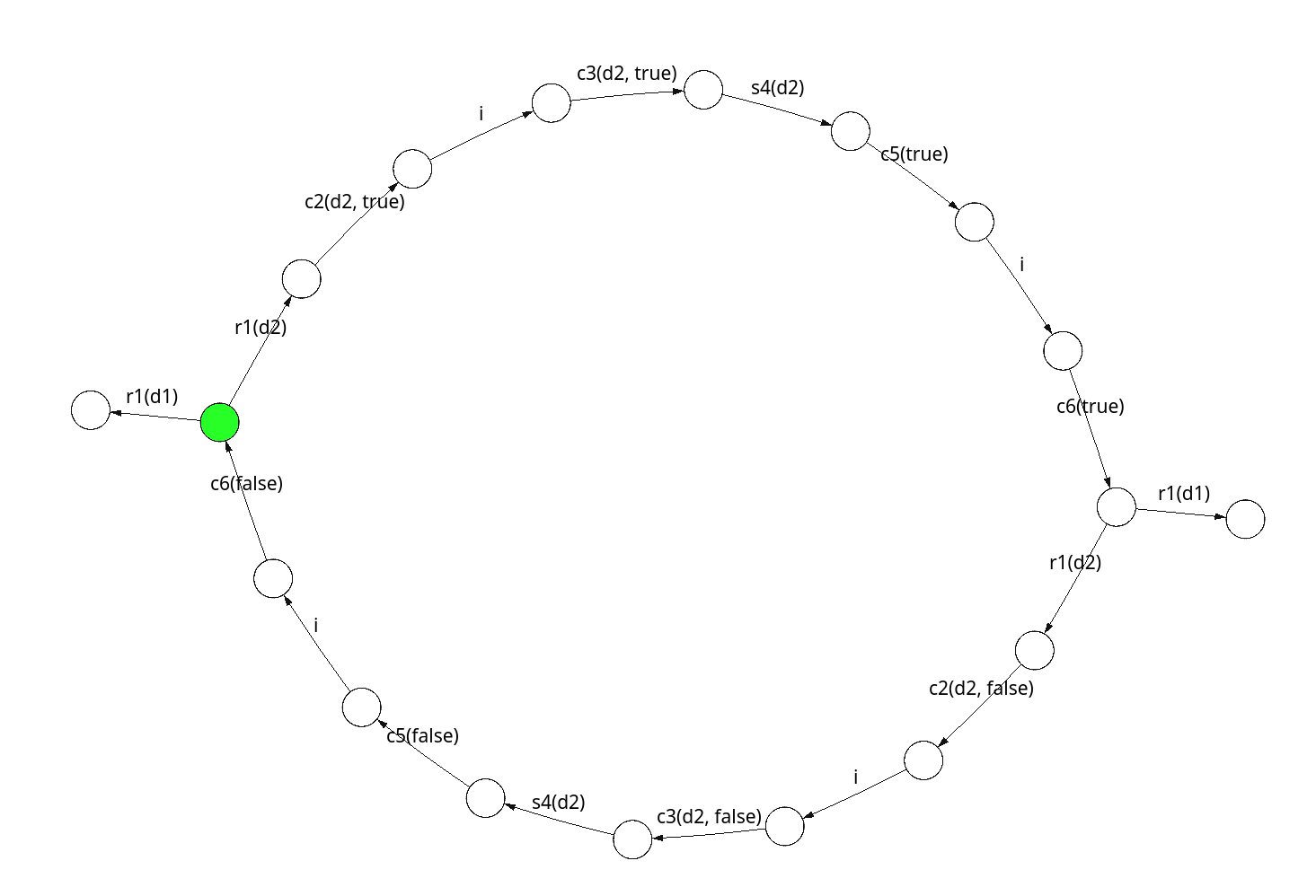
Counter example for the property “infinitely often enabled then infinitely often taken”.

Note

The interface of pbessolve is not stable yet. In particular the strategies that are available through the option -s are subject to change.

orphan:

---

Usage

pbessolve   [OPTION]... [INFILE]

Description

Solves (P)BES from INFILE. If INFILE is not present, stdin is used. The PBES is first instantiated into a parity game, which is then solved using Zielonka’s algorithm. It supports the generation of a witness or counter example for the property encoded by the PBES.

Command line options

--evidence-file=NAME

The file to which the evidence is written. If not set, a default name will be chosen.

-fNAME , --file=NAME

The file containing the LPS or LTS that was used to generate the PBES using lps2pbes -c. If this option is set, a counter example or witness for the encoded property will be generated. The extension of the file should be .lps in case of an LPS file, in all other cases it is assumed to be an LTS.

-iFORMAT , --in=FORMAT

use input format FORMAT:

pbes

PBES in internal format

--prune-todo-list

Prune the todo list periodically.

-QNUM , --qlimit=NUM

limit enumeration of quantifiers to NUM iterations. (Default NUM=1000, NUM=0 for unlimited).

-rNAME , --rewriter=NAME

use rewrite strategy NAME:

jitty

jitty rewriting

jittyc

compiled jitty rewriting

jittyp

jitty rewriting with prover

-zNAME , --search-strategy=NAME

Use search strategy NAME:

breadth-first

Leads to smaller counter examples

depth-first

-sNAME , --solve-strategy=NAME

Use solve strategy NAME. Strategies 1-4 periodically apply on-the-fly solving, which may lead to early termination.

0

No on-the-fly solving is applied

1

Propagate solved equations using an attractor.

2

Detect winning loops.

3

Solve subgames using a fatal attractor.

4

Solve subgames using the solver.

--threads=NUM

run with NUM threads (default=1). With multiple threads the stack size on a Mac is limited which can lead to bus errors.

--timings[=FILE]

append timing measurements to FILE. Measurements are written to standard error if no FILE is provided

Standard options

-q , --quiet

do not display warning messages

-v , --verbose

display short log messages

-d , --debug

display detailed log messages

--log-level=LEVEL

display log messages up to and including level; either warn, verbose, debug or trace

-h , --help

display help information

--version

display version information

--help-all

display help information, including hidden and experimental options

Author

Wieger Wesselink